treedp

👾树形动态规划

==树形动态规划，即在树上进行的动态规划。==

==因为树的递归性质，树形动态规划一般都是递归求解的。==

🫐[P1352]没有上司的舞会

没有上司的舞会

题目描述

某大学有 $n$ 个职员，编号为 $1\dots n$。

他们之间有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。

现在有个周年庆宴会，宴会每邀请来一个职员都会增加一定的快乐指数 $r_i$，但是呢，如果某个职员的直接上司来参加舞会了，那么这个职员就无论如何也不肯来参加舞会了。

所以，请你编程计算，邀请哪些职员可以使快乐指数最大，求最大的快乐指数。

输入格式

输入的第一行是一个整数 $n$。

第 $2$ 到第 $(n+1)$ 行，每行一个整数，第 $(i+1)$ 行的整数表示 $i$ 号职员的快乐指数 $r_i$。

第 $(n+2)$ 到第 $2n$ 行，每行输入一对整数 $l,k$，代表 $k$ 是 $l$ 的直接上司。

输出格式

输出一行一个整数代表最大的快乐指数。

样例 #1

样例输入 #1

7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5

样例输出 #1

5

提示

数据规模与约定

对于 $100\%$ 的数据，保证 $1\le n\le 6\times 10^3$，$-128\le r_i\le 127$，$1\le l,k\le n$，且给出的关系一定是一棵树。

🫐[P1040]加分二叉树

[NOIP2003 提高组] 加分二叉树

题目描述

设一个 $n$ 个节点的二叉树 $\text{tree}$ 的中序遍历为$(1,2,3,\dots ,n)$，其中数字 $1,2,3,\dots ,n$ 为节点编号。每个节点都有一个分数（均为正整数），记第 $i$ 个节点的分数为 $d_i$，$\text{tree}$ 及它的每个子树都有一个加分，任一棵子树 $\text{subtree}$（也包含 $\text{tree}$ 本身）的加分计算方法如下：

$\text{subtree}$ 的左子树的加分 $\times$ $\text{subtree}$ 的右子树的加分 $+$ $\text{subtree}$ 的根的分数。

若某个子树为空，规定其加分为 $1$，叶子的加分就是叶节点本身的分数。不考虑它的空子树。

试求一棵符合中序遍历为 $(1,2,3,\dots ,n)$ 且加分最高的二叉树 $\text{tree}$。要求输出

1. $\text{tree}$ 的最高加分。

2. $\text{tree}$ 的前序遍历。

输入格式

第 $1$ 行 $1$ 个整数 $n$，为节点个数。

第 $2$ 行 $n$ 个用空格隔开的整数，为每个节点的分数

输出格式

第 $1$ 行 $1$ 个整数，为最高加分（$Ans\le 4,000,000,000$）。

第 $2$ 行 $n$ 个用空格隔开的整数，为该树的前序遍历。

样例 #1

样例输入 #1

5
5 7 1 2 10

样例输出 #1

145
3 1 2 4 5

提示

数据规模与约定

对于全部的测试点，保证 $1\le n<30$，节点的分数是小于 $100$ 的正整数，答案不超过 $4\times 10^9$。

🫐[P1122]最大子树和

最大子树和

题目描述

小明对数学饱有兴趣，并且是个勤奋好学的学生，总是在课后留在教室向老师请教一些问题。一天他早晨骑车去上课，路上见到一个老伯正在修剪花花草草，顿时想到了一个有关修剪花卉的问题。于是当日课后，小明就向老师提出了这个问题：

一株奇怪的花卉，上面共连有 $N$ 朵花，共有 $N-1$ 条枝干将花儿连在一起，并且未修剪时每朵花都不是孤立的。每朵花都有一个“美丽指数”，该数越大说明这朵花越漂亮，也有“美丽指数”为负数的，说明这朵花看着都让人恶心。所谓“修剪”，意为：去掉其中的一条枝条，这样一株花就成了两株，扔掉其中一株。经过一系列“修剪“之后，还剩下最后一株花（也可能是一朵）。老师的任务就是：通过一系列“修剪”（也可以什么“修剪”都不进行），使剩下的那株（那朵）花卉上所有花朵的“美丽指数”之和最大。

老师想了一会儿，给出了正解。小明见问题被轻易攻破，相当不爽，于是又拿来问你。

输入格式

第一行一个整数 $n(1\le N\le 16000)$。表示原始的那株花卉上共 $n$ 朵花。

第二行有 $n$ 个整数，第 $i$ 个整数表示第 $i$ 朵花的美丽指数。

接下来 $n-1$ 行每行两个整数 $a,b$，表示存在一条连接第 $a$ 朵花和第 $b$ 朵花的枝条。

输出格式

一个数，表示一系列“修剪”之后所能得到的“美丽指数”之和的最大值。保证绝对值不超过 $2147483647$。

样例 #1

样例输入 #1

7
-1 -1 -1 1 1 1 0
1 4
2 5
3 6
4 7
5 7
6 7

样例输出 #1

3

提示

数据范围及约定

• 对于 $60\%$ 的数据，有 $1\le N\le 1000$；
• 对于 $100\%$ 的数据，有 $1\le N\le 16000$。

🫐[P1273]有线电视网

有线电视网

题目描述

某收费有线电视网计划转播一场重要的足球比赛。他们的转播网和用户终端构成一棵树状结构，这棵树的根结点位于足球比赛的现场，树叶为各个用户终端，其他中转站为该树的内部节点。

从转播站到转播站以及从转播站到所有用户终端的信号传输费用都是已知的，一场转播的总费用等于传输信号的费用总和。

现在每个用户都准备了一笔费用想观看这场精彩的足球比赛，有线电视网有权决定给哪些用户提供信号而不给哪些用户提供信号。

写一个程序找出一个方案使得有线电视网在不亏本的情况下使观看转播的用户尽可能多。

输入格式

输入文件的第一行包含两个用空格隔开的整数 $N$ 和 $M$，其中 $2\le N\le 3000$，$1\le M\le N-1$，$N$ 为整个有线电视网的结点总数，$M$ 为用户终端的数量。

第一个转播站即树的根结点编号为 $1$，其他的转播站编号为 $2$ 到 $N-M$，用户终端编号为 $N-M+1$ 到 $N$。

接下来的 $N-M$ 行每行表示—个转播站的数据，第 $i+1$ 行表示第 $i$ 个转播站的数据，其格式如下：

$K{A}_1{C}_1{A}_2{C}_2\dots A_k{C}_k$

$K$ 表示该转播站下接 $K$ 个结点（转播站或用户），每个结点对应一对整数 $A$ 与 $C$ ，$A$ 表示结点编号，$C$ 表示从当前转播站传输信号到结点 $A$ 的费用。最后一行依次表示所有用户为观看比赛而准备支付的钱数。单次传输成本和用户愿意交的费用均不超过 10。

输出格式

输出文件仅一行，包含一个整数，表示上述问题所要求的最大用户数。

样例 #1

样例输入 #1

5 3
2 2 2 5 3
2 3 2 4 3
3 4 2

样例输出 #1

2

提示

样例解释

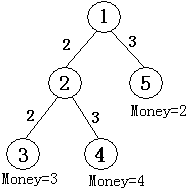
如图所示，共有五个结点。结点 ① 为根结点，即现场直播站，② 为一个中转站，③④⑤ 为用户端，共 $M$ 个，编号从 $N-M+1$ 到 $N$，他们为观看比赛分别准备的钱数为 $3$、$4$、$2$。

从结点 ① 可以传送信号到结点 ②，费用为 $2$；

也可以传送信号到结点 ⑤，费用为 $3$（第二行数据所示）；

从结点 ② 可以传输信号到结点 ③，费用为$2$；

也可传输信号到结点 ④，费用为 $3$（第三行数据所示）。

如果要让所有用户（③④⑤）都能看上比赛，则信号传输的总费用为：$2+3+2+3=10$，大于用户愿意支付的总费用 $3+4+2=9$，有线电视网就亏本了，而只让 ③④ 两个用户看比赛就不亏本了。

🫐[P2014]选课

[CTSC1997] 选课

题目描述

在大学里每个学生，为了达到一定的学分，必须从很多课程里选择一些课程来学习，在课程里有些课程必须在某些课程之前学习，如高等数学总是在其它课程之前学习。现在有 $N$ 门功课，每门课有个学分，每门课有一门或没有直接先修课（若课程 a 是课程 b 的先修课即只有学完了课程 a，才能学习课程 b）。一个学生要从这些课程里选择 $M$ 门课程学习，问他能获得的最大学分是多少？

输入格式

第一行有两个整数 $N$ , $M$ 用空格隔开。( $1\le N\le 300$ , $1\le M\le 300$ )

接下来的 $N$ 行,第 $I+1$ 行包含两个整数 $k_i$和 $s_i$, $k_i$ 表示第I门课的直接先修课，$s_i$ 表示第I门课的学分。若 $k_i=0$ 表示没有直接先修课（$1\le k_i\le N$ , $1\le s_i\le 20$）。

输出格式

只有一行，选 $M$ 门课程的最大得分。

样例 #1

样例输入 #1

7  4
2  2
0  1
0  4
2  1
7  1
7  6
2  2

样例输出 #1

13

🫐[P2585]三色二叉树

[ZJOI2006] 三色二叉树

题目描述

一棵二叉树可以按照如下规则表示成一个由 $0$、$1$、$2$ 组成的字符序列，我们称之为“二叉树序列 $S$”：

\begin{cases} 0& \text{表示该树没有子节点}\\ 1S_1& \text{表示该树有一个节点，}S_1 \text{为其子树的二叉树序列}\\ 2S_1S_2& \text{表示该树由两个子节点，}S_1 \text{和} S_2 \text{分别表示其两个子树的二叉树序列} \end{cases}$$ 例如，下图所表示的二叉树可以用二叉树序列 $S=\texttt{21200110}$ 来表示。 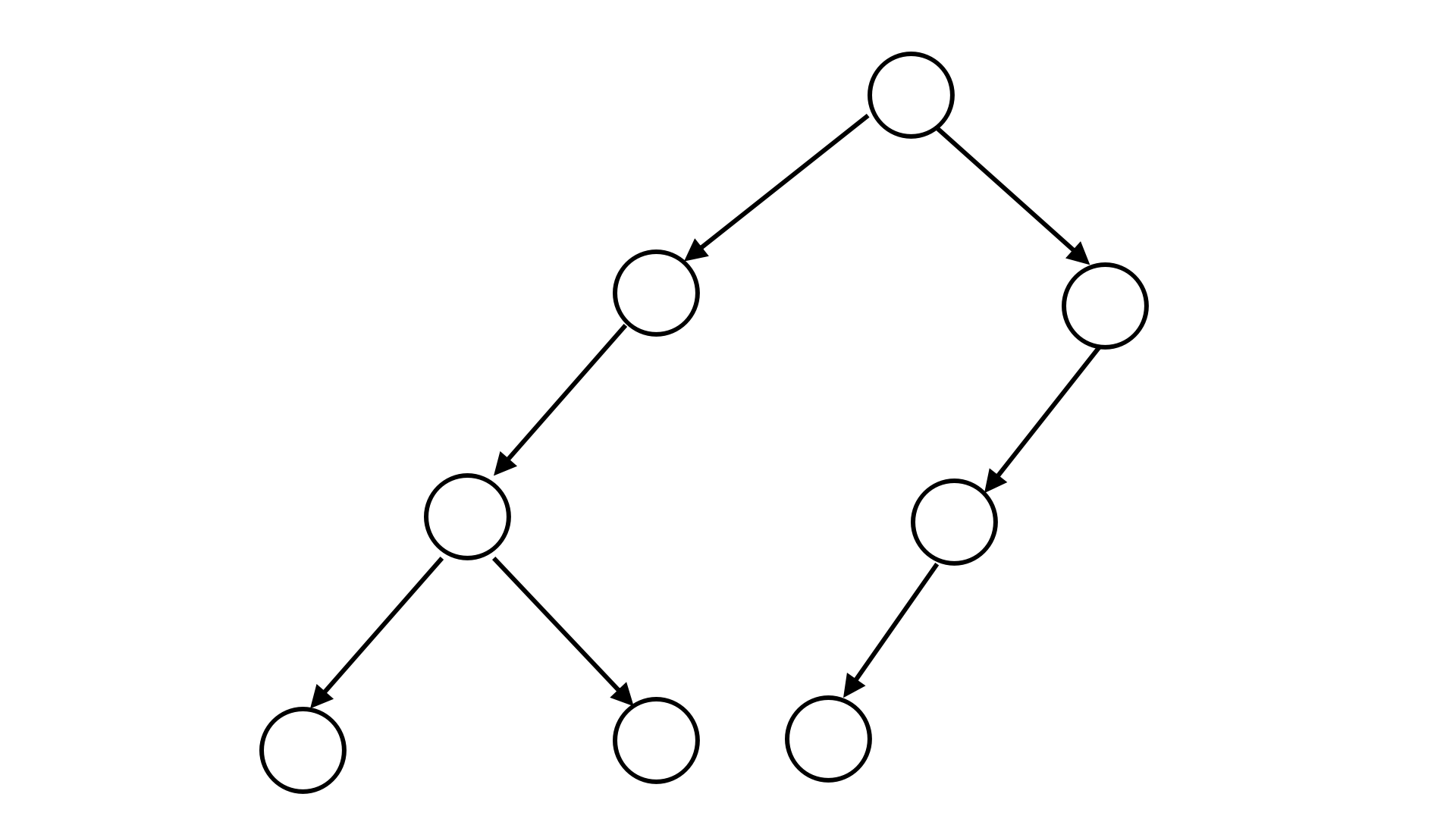 你的任务是要对一棵二叉树的节点进行染色。每个节点可以被染成红色、绿色或蓝色。并且，一个节点与其子节点的颜色必须不同，如果该节点有两个子节点，那么这两个子节点的颜色也必须不同。给定一颗二叉树的二叉树序列，请求出这棵树中**最多和最少**有多少个点能够被染成绿色。 ## 输入格式 输入只有一行一个字符串 $s$，表示二叉树序列。 ## 输出格式 输出只有一行，包含两个数，依次表示最多和最少有多少个点能够被染成绿色。 ## 样例 #1 ### 样例输入 #1 ``` 1122002010 ``` ### 样例输出 #1 ``` 5 2 ``` ## 提示 #### 数据规模与约定 对于全部的测试点，保证 $1 \leq |s| \leq 5 \times 10^5$，$s$ 中只含字符 `0` `1` `2`。

🫐[P3047 ]Nearby Cows

[USACO12FEB] Nearby Cows G

题目描述

Farmer John has noticed that his cows often move between nearby fields. Taking this into account, he wants to plant enough grass in each of his fields not only for the cows situated initially in that field, but also for cows visiting from nearby fields.

Specifically, FJ’s farm consists of N fields (1 ⇐ N ⇐ 100,000), where some pairs of fields are connected with bi-directional trails (N-1 of them in total). FJ has designed the farm so that between any two fields i and j, there is a unique path made up of trails connecting between i and j. Field i is home to C(i) cows, although cows sometimes move to a different field by crossing up to K trails (1 ⇐ K ⇐ 20).

FJ wants to plant enough grass in each field i to feed the maximum number of cows, M(i), that could possibly end up in that field — that is, the number of cows that can potentially reach field i by following at most K trails. Given the structure of FJ’s farm and the value of C(i) for each field i, please help FJ compute M(i) for every field i.

给你一棵 $n$ 个点的树，点带权，对于每个节点求出距离它不超过 $k$ 的所有节点权值和 $m_i$。

输入格式

* Line 1: Two space-separated integers, N and K.

* Lines 2..N: Each line contains two space-separated integers, i and j (1 ⇐ i,j ⇐ N) indicating that fields i and j are directly connected by a trail.

* Lines N+1..2N: Line N+i contains the integer C(i). (0 ⇐ C(i) ⇐ 1000)

第一行两个正整数 $n,k$。
接下来 $n-1$ 行，每行两个正整数 $u,v$，表示 $u,v$ 之间有一条边。
最后 $n$ 行，每行一个非负整数 $c_i$，表示点权。

输出格式

* Lines 1..N: Line i should contain the value of M(i).

输出 $n$ 行，第 $i$ 行一个整数表示 $m_i$。

样例 #1

样例输入 #1

6 2 
5 1 
3 6 
2 4 
2 1 
3 2 
1 
2 
3 
4 
5 
6

样例输出 #1

15 
21 
16 
10 
8 
11

提示

There are 6 fields, with trails connecting (5,1), (3,6), (2,4), (2,1), and (3,2). Field i has C(i) = i cows.

Field 1 has M(1) = 15 cows within a distance of 2 trails, etc.

【数据范围】
对于 $100\%$ 的数据：$1\le n\le 10^5$，$1\le k\le 20$，$0\le c_i\le 1000$

🫐[P3698]小Q的棋盘

[CQOI2017] 小Q的棋盘

题目描述

小 Q 正在设计一种棋类游戏。

在小 Q 设计的游戏中，棋子可以放在棋盘上的格点中。某些格点之间有连线，棋子只能在有连线的格点之间移动。整个棋盘上共有 $V$ 个格点，编号为 $0,1,2,\cdots ,V-1$，它们是连通的，也就是说棋子从任意格点出发，总能到达所有的格点。小 Q 在设计棋盘时，还保证棋子从一个格点移动到另外任一格点的路径是唯一的。

小 Q 现在想知道，当棋子从格点 $0$ 出发，移动 $N$ 步最多能经过多少格点。格点可以重复经过多次，但不重复计数。

输入格式

第一行包含2个正整数 $V,N$，其中 $V$ 表示格点总数，$N$ 表示移动步数。

接下来 $V-1$ 行，每行两个数 $a_i,b_i$，表示编号为$a_i,b_i$ 的两个格点之间有连线。

输出格式

输出一行一个整数，表示最多经过的格点数量。

样例 #1

样例输入 #1

5 2
1 0
2 1
3 2
4 3

样例输出 #1

3

样例 #2

样例输入 #2

9 5
0 1
0 2
2 6
4 2
8 1
1 3
3 7
3 5

样例输出 #2

5

提示

【输入输出样例 1 说明】

从格点 $0$ 出发移动 $2$ 步。经过 $0,1,2$ 这 $3$ 个格点。

【输入输出样例 2 说明】

一种可行的移动路径为 $0\to 1\to 3\to 5\to 3\to 7$，经过 $0,1,3,5,7$ 这 $5$ 个格点。

【数据规模与约定】

对于 $100\%$ 的测试点，$1\le N,V\le 100$，$0\le a_i,b_i<V$。

🫐[P5658]括号树

[CSP-S2019] 括号树

题目背景

本题中合法括号串的定义如下：

1. () 是合法括号串。
2. 如果 A 是合法括号串，则 (A) 是合法括号串。
3. 如果 A，B 是合法括号串，则 AB 是合法括号串。

本题中子串与不同的子串的定义如下：

1. 字符串 S 的子串是 S 中连续的任意个字符组成的字符串。S 的子串可用起始位置 $l$ 与终止位置 $r$ 来表示，记为 $S(l,r)$（$1\le l\le r\le |S|$，$|S|$ 表示 S 的长度）。
2. S 的两个子串视作不同当且仅当它们在 S 中的位置不同，即 $l$ 不同或 $r$ 不同。

题目描述

一个大小为 $n$ 的树包含 $n$ 个结点和 $n-1$ 条边，每条边连接两个结点，且任意两个结点间有且仅有一条简单路径互相可达。

小 Q 是一个充满好奇心的小朋友，有一天他在上学的路上碰见了一个大小为 $n$ 的树，树上结点从 $1\sim n$ 编号，$1$ 号结点为树的根。除 $1$ 号结点外，每个结点有一个父亲结点，$u$（$2\le u\le n$）号结点的父亲为 $f_u$（$1\le f_u<u$）号结点。

小 Q 发现这个树的每个结点上恰有一个括号，可能是( 或)。小 Q 定义 $s_i$ 为：将根结点到 $i$ 号结点的简单路径上的括号，按结点经过顺序依次排列组成的字符串。

显然 $s_i$ 是个括号串，但不一定是合法括号串，因此现在小 Q 想对所有的 $i$（$1\le i\le n$）求出，$s_i$ 中有多少个互不相同的子串是合法括号串。

这个问题难倒了小 Q，他只好向你求助。设 $s_i$ 共有 $k_i$ 个不同子串是合法括号串， 你只需要告诉小 Q 所有 $i\times k_i$ 的异或和，即： $(1\times k_1)\text{xor}(2\times k_2)\text{xor}(3\times k_3)\text{xor}\cdots \text{xor}(n\times k_n)$ 其中 $xor$ 是位异或运算。

输入格式

第一行一个整数 $n$，表示树的大小。

第二行一个长为 $n$ 的由( 与) 组成的括号串，第 $i$ 个括号表示 $i$ 号结点上的括号。

第三行包含 $n-1$ 个整数，第 $i$（$1\le i<n$）个整数表示 $i+1$ 号结点的父亲编号 $f_{i+1}$。

输出格式

仅一行一个整数表示答案。

样例 #1

样例输入 #1

5
(()()
1 1 2 2

样例输出 #1

6

提示

【样例解释1】

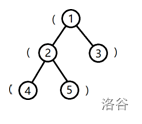
树的形态如下图：

将根到 1 号结点的简单路径上的括号，按经过顺序排列所组成的字符串为 (，子串是合法括号串的个数为 $0$。

将根到 2 号结点的字符串为 ((，子串是合法括号串的个数为 $0$。

将根到 3 号结点的字符串为 ()，子串是合法括号串的个数为 $1$。

将根到 4 号结点的字符串为 (((，子串是合法括号串的个数为 $0$。

将根到 5 号结点的字符串为 (()，子串是合法括号串的个数为 $1$。

【数据范围】

🫐[P2607]骑士

[ZJOI2008] 骑士

题目描述

Z 国的骑士团是一个很有势力的组织，帮会中汇聚了来自各地的精英。他们劫富济贫，惩恶扬善，受到社会各界的赞扬。

最近发生了一件可怕的事情，邪恶的 Y 国发动了一场针对 Z 国的侵略战争。战火绵延五百里，在和平环境中安逸了数百年的 Z 国又怎能抵挡的住 Y 国的军队。于是人们把所有的希望都寄托在了骑士团的身上，就像期待有一个真龙天子的降生，带领正义打败邪恶。

骑士团是肯定具有打败邪恶势力的能力的，但是骑士们互相之间往往有一些矛盾。每个骑士都有且仅有一个自己最厌恶的骑士（当然不是他自己），他是绝对不会与自己最厌恶的人一同出征的。

战火绵延，人民生灵涂炭，组织起一个骑士军团加入战斗刻不容缓！国王交给了你一个艰巨的任务，从所有的骑士中选出一个骑士军团，使得军团内没有矛盾的两人（不存在一个骑士与他最痛恨的人一同被选入骑士军团的情况），并且，使得这支骑士军团最具有战斗力。

为了描述战斗力，我们将骑士按照 $1$ 至 $n$ 编号，给每名骑士一个战斗力的估计，一个军团的战斗力为所有骑士的战斗力总和。

输入格式

第一行包含一个整数 $n$，描述骑士团的人数。

接下来 $n$ 行，每行两个整数，按顺序描述每一名骑士的战斗力和他最痛恨的骑士。

输出格式

应输出一行，包含一个整数，表示你所选出的骑士军团的战斗力。

样例 #1

样例输入 #1

3
10 2
20 3
30 1

样例输出 #1

30

提示

数据规模与约定

对于 $30\%$ 的测试数据，满足 $n\le 10$；

对于 $60\%$ 的测试数据，满足 $n\le 100$；

对于 $80\%$ 的测试数据，满足 $n\le 10^4$。

对于 $100\%$ 的测试数据，满足 $1\le n\le 10^6$，每名骑士的战斗力都是不大于 $10^6$ 的正整数。

🫐[P3177]树上染色

[HAOI2015] 树上染色

题目描述

有一棵点数为 $n$ 的树，树边有边权。给你一个在 $0\sim n$ 之内的正整数 $k$ ，你要在这棵树中选择 $k$ 个点，将其染成黑色，并将其他的 $n-k$ 个点染成白色。将所有点染色后，你会获得黑点两两之间的距离加上白点两两之间的距离的和的收益。问收益最大值是多少。

输入格式

第一行包含两个整数 $n,k$。

第二到 $n$ 行每行三个正整数 $u,v,w$，表示该树中存在一条长度为 $w$ 的边 $(u,v)$。输入保证所有点之间是联通的。

输出格式

输出一个正整数，表示收益的最大值。

样例 #1

样例输入 #1

3 1
1 2 1
1 3 2

样例输出 #1

3

提示

对于 $100\%$ 的数据，$0\le n,k\le 2000$。

🫐[P4395]Gem

[BOI2003] Gem 气垫车

题目描述

给出一棵树，要求你为树上的结点标上权值，权值可以是任意的正整数

唯一的限制条件是相临的两个结点不能标上相同的权值，要求一种方案，使得整棵树的总价值最小。

输入格式

先给出一个数字N,代表树上有N个点,N⇐10000

下面N-1行,代表两个点相连

输出格式

最小的总权值

样例 #1

样例输入 #1

10 
7 5 
1 2 
1 7 
8 9 
4 1 
9 7 
5 6 
10 2 
9 3

样例输出 #1

14

提示

本题已经添加数据，但考虑到题目年代较为久远（毕竟是2003年的BOI了）以及洛谷神速评测姬，将此题时限修改为500ms。

🫐[P4516]潜入行动

[JSOI2018] 潜入行动

题目描述

外星人又双叒叕要攻打地球了，外星母舰已经向地球航行！这一次，JYY 已经联系好了黄金舰队，打算联合所有 JSOIer 抵御外星人的进攻。

在黄金舰队就位之前，JYY 打算事先了解外星人的进攻计划。现在，携带了监听设备的特工已经秘密潜入了外星人的母舰，准备对外星人的通信实施监听。

外星人的母舰可以看成是一棵 $n$ 个节点、 $n-1$ 条边的无向树，树上的节点用 $1,2,\cdots ,n$ 编号。JYY 的特工已经装备了隐形模块，可以在外星人母舰中不受限制地活动，可以神不知鬼不觉地在节点上安装监听设备。

如果在节点 $u$ 上安装监听设备，则 JYY 能够监听与 $u$ 直接相邻所有的节点的通信。换言之，如果在节点 $u$ 安装监听设备，则对于树中每一条边 $(u,v)$ ，节点 $v$ 都会被监听。特别注意放置在节点 $u$ 的监听设备并不监听 $u$ 本身的通信，这是 JYY 特别为了防止外星人察觉部署的战术。

JYY 的特工一共携带了 $k$ 个监听设备，现在 JYY 想知道，有多少种不同的放置监听设备的方法，能够使得母舰上所有节点的通信都被监听？为了避免浪费，每个节点至多只能安装一个监听设备，且监听设备必须被用完。

输入格式

输入第一行包含两个整数 $n,k$ ，表示母舰节点的数量 $n$ 和监听设备的数量 $k$ 。 接下来 $n-1$ 行，每行两个整数 $u,v$ $(1\le u,v\le n)$，表示树中的一条边。

输出格式

输出一行，表示满足条件的方案数。因为答案可能很大，你只需要输出答案 $\text{mod 1,000,000,007}$ 的余数即可。

样例 #1

样例输入 #1

5 3
1 2
2 3
3 4
4 5

样例输出 #1

1

提示

样例 1 解释

样例数据是一条链 $1-2-3-4-5$ 。首先，节点 $2$ 和 $4$ 必须放置监听设备，否则 $1,5$ 将无法被监听（放置的监听设备无法监听它所在的节点）。剩下一个设备必须放置在 $3$ 号节点以同时监听 $2,4$ 。因此在 $2,3,4$ 节点放置监听设备是唯一合法的方案。

数据范围

存在 $10\%$ 的数据，$1\le n\le 20$ ；

存在另外 $10\%$ 的数据，$1\le n\le 100$ ；

存在另外 $10\%$ 的数据，$1\le k\le 10$ ；

存在另外 $10\%$ 的数据，输入的树保证是一条链；

对于所有数据，$1\le n\le 10^5$ ，$1\le k\le \min \{n,100\}$ 。